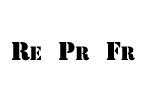2016-11-19

Метод последовательных приближений в гидравлике

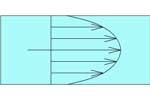
Достаточно часто в гидравлических расчетах необходимо вычислить скорость течения жидкости, при неизвестных сопротивлениях, а значит и неизвестно рабочей точке насоса. Коэффициенты сопротивления необходимы для расчета скорости, но в свою очередь они зависят не только от геометрии но и от числа Рейнольдса (Re), который определяется по скорости. Такие задачи решаются методом последовательных приближений или графоаналитически.

Расчет в первом приближении

Метод последовательных приближений построен на том, что большинство гидравлических коэффициентов при больших числах Рейнольдса (Re) зависят от пограничной геометрии, поэтому в первом приближении задачу решают при коэффициентах найденных в зоне автомодельности (т.е. при больших числах Рейнольдса). По скорости найденной в первом приближении определяется число Рейнольдса.

Расчет во втором приближении

Во втором приближении по числу Рейнольдса и геометрии находим гидравлические коэффициенты, затем вычисляем скорость во втором приближении.

Определение и оценка погрешности

Далее определяем относительную погрешность:

Если полученное значение удовлетворяет требованиям, то вычисления окончены. Если нет, то делаем третье приближение, и так далее.